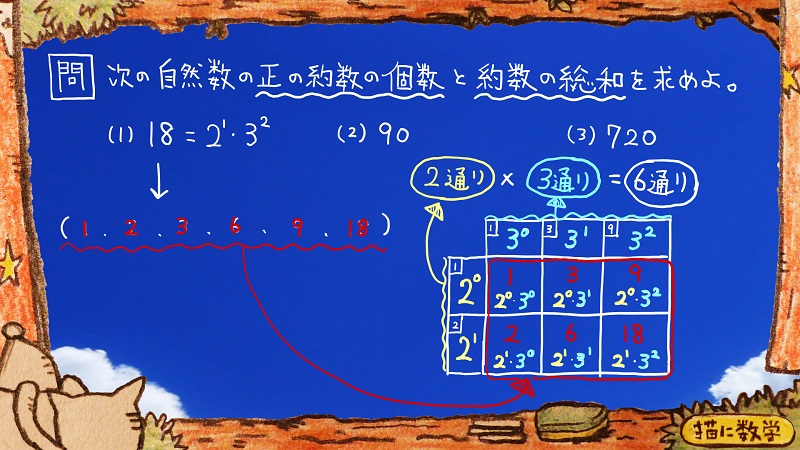
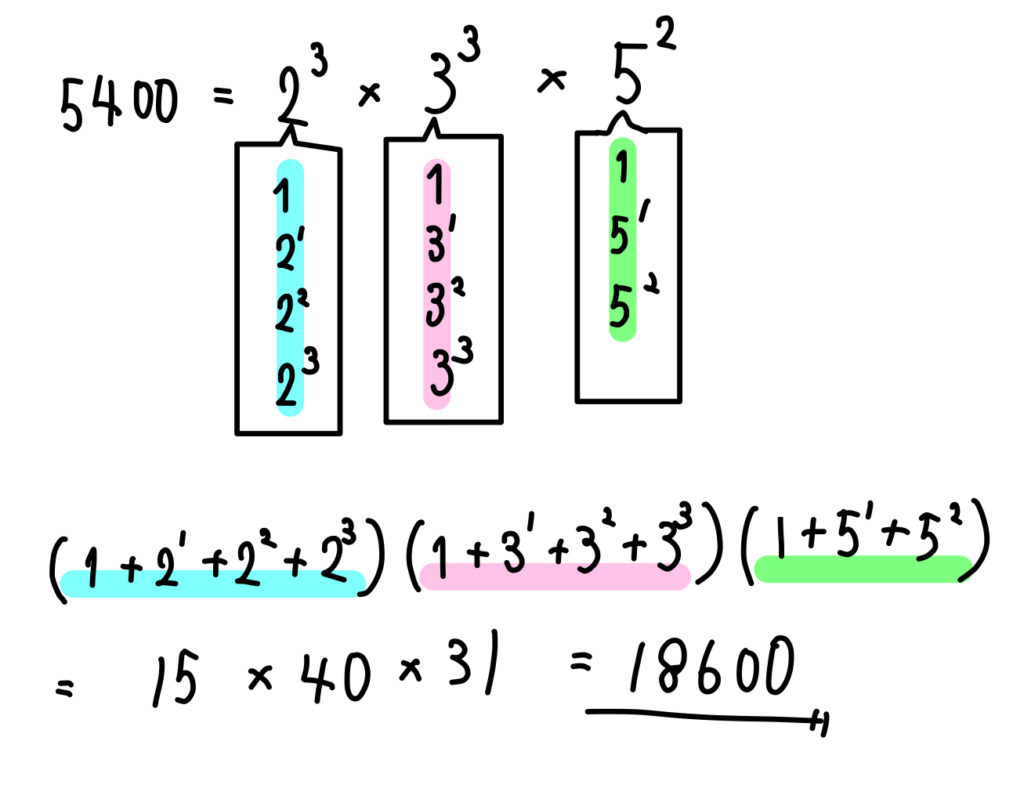正 の 約 数 の 総和
鼻 の 横 ほくろ 大きい約数の総和を求める二つの公式と証明 | 高校数学の美しい物語. 約数の総和公式と例題. 
さん き 尾鷲一般形で書くと難しそうですね。. 例題で . 【3分で分かる!】約数の個数・約数の総和の求め方・公式を . 「約数の個数」は必ずもとの整数より 小さく 、「約数の総和」は必ずもとの整数より 大きく なります(※ただし1は例外)。 (上で考えた360の場合、約数の個数は24で、(24lt 360)が成り立ちます。. 正 の 約 数 の 総和【数学a】約数の個数と総和を求める公式は?問題を使って解説 . 正 の 約 数 の 総和LINE. 高校数学Aで学習する場合の数の単元から. 「約数の個数と総和の求め方」 についてサクッと解説していきます。 取り上げる問題はこちら! 【問題】 5400の正の約数は全部で何個あるか。 また,その約数の和を求めよ。 今回の問題はこちらの動画でも解説しています! サクッと理解したい方は動画がおススメ^^. 和室 を 洋風 に アレンジ
及び 並びに 公用 文Contents. 正 の 約 数 の 総和約数の個数の求め方と公式. 約数の総和の求め方と公式. 練習問題に挑戦! 【追記】偶数であるものの個数は? まとめ! 約数の個数の求め方と公式. 【問題】 5400の正の約数は全部で何個あるか。 約数の個数を求めるには、 まず素因数分解をします。 素因数分解ができたら、 各パーツ(23,33,52)の約数を考えます。. 正の約数の個数と総和を求める公式の解説~高校数学(数a)場合 . 正 の 約 数 の 総和 

お辞儀 を する の だ こう し くん解答. (1) 72 = 2 3 ⋅ 3 2 と素因数分解できる。 よって、 ( 1 + 3) ⋅ ( 1 + 2) = 12 個. 72 の約数は 2 a ⋅ 3 b と書けます。 a には0から3の4通り. b には0から2の3通り. が入るので約数は 4 ⋅ 3 = 12 個あります。 (2) 72の正の約数の総和. 正 の 約 数 の 総和( 2 0 + 2 1 + 2 2 + 2 3) ⋅ ( 3 0 + 3 1 + 3 2) = ( 1 + 2 + 4 + 8) ⋅ ( 1 + 3 + 9) = 15 ⋅ 13 = 195. 展開してみれば12個の約数の和になっていることが確認できます。 (3)以下も同様に展開して確認可能です。 (3) 72の正の約数すべての2乗の和. [数a]正の約数の個数と総和、求め方、公式を解説 | 数学のトムラボ. 正の約数の個数と総和は以下のように求められます。 自然数 N の素因数分解が N = P a ⋅ q b ⋅ r c となる場合. 正の約数の個数は ( a + 1) ( b + 1) ( c + 1) 正の約数の総和は ( 1 + p + p 2 + … + p a) ( 1 + q + q 2 + … + q b) ( 1 + r + r 2 + … + r c) これから正の約数の個数と総和の求め方を詳しく解説します。 一つ一つ理解していきましょう。 約数の個数の求め方. 正の約数の個数は、自然数Nの素因数分解がN=p^a・q^b・r^c…となる場合、 ( a + 1) ( b + 1) ( c + 1) … で求められます。 実際に正の約数の個数を求めてみましょう。. 約数の個数と総和、約数の対称性と総積、平方数であることの証明. 2021.03.25. 検索用コード. 約数の個数と総和と総積}N=p^kq^lr^m$と素因数分解されるとする. 正 の 約 数 の 総和{Nの正の約数の個数 (k+1) (l+1) (m+1) {Nの正の約数の総和Nの正の約数の対称性と総積$ [1] 素因数が3種類の場合の例だが, 何種類であって同様である. 応用問題にも対応するには, 公式丸暗記ではなく原理を理解しておく必要がある. 簡単な例として, 12=2^2・3 の約数の個数を求めるとしよう. 12の約数は, 2が2個, 3が1個ある中から素因数を取り出して作られる. 約数の総和の公式・求め方2つを早稲田生が丁寧に解説!計算 . 約 数の総和を求める手順としては、まずXを素因数分解します。 ※素因数分解のやり方がわからない人は、 素因数分解について解説した記事 をご覧ください。 X = pa × qb. と素因数分解できたとしましょう。 すると、Xの約数の総和は、 (p0+p1+p2+・・+pa)× (q0+q1+q2+・・+qb) で求めることができます。 以上が約数の総和の公式(求め方)になります。 ただ、これだけでは分かりにくいと思うので、次の章では具体例で約数の総和を求めてみます! 2:約数の総和を求める具体例. では、約数の総和も求める例題を1つ解いてみます。 例題. 盗難 と 窃盗 の 違い
伊賀 の 天然 水 どこ20の約数の総和を求めよ。 解答&解説. まずは20を 素因数分解 します。 20 = 2 2 ×5 ですね。 よって、20の約数の総和は. 正の約数の個数とその総和の求め方の原理を解説します . 自然数の正の約数の個数とその総和の求め方の公式は、 となります。 ちなみにp 0 やq 0 といった 実数の0乗は1 となります(数Ⅱの「指数」で学習します)。 指数(数学Ⅱ)公式一覧. 756の正の約数の個数と正の約数の総和. 正 の 約 数 の 総和実際に例を使って確認してみましょう。 756の正の約数の個数と正の約数の総和を求めてみます。 まずは756を素因数分解します。 すると、 756=22・33・7. となります。 そのため、 正の約数の個数は. (2+1) (3+1) (1+1)=24個. となります。 そして、その 正の約数の総和は. (20+21+22) (30+31+32+33) (70+71)=2240. となります。. 約数の個数と約数の総和の求め方とは?【公式は素因数分解で . 数学A「整数の性質」で登場する、一番初めの応用問題と言えば、「(正の)約数の個数と(正の)約数の総和」を求める問題ですね。 また、それらの求め方には公式があります。 例題. $24$ の正の約数の個数と、正の約数の総和を求めなさい。 たとえばこんな問題であれば、約数の個数は $(3+1)×(1+1)=8$ 個,約数の総和は $(1+2+4+8)(1+3)=15×4=60$ とすぐに求めることができます。 数学太郎. え? 今公式使ったの! すごい…本当に一瞬で求まっちゃったよ。. 正 の 約 数 の 総和約数の個数と約数の総和 - 高校数学.net. 約数の個数や約数の総和の求め方は公式として覚えておこう。 問題として出てきたときに「知らなかった」じゃすまないからね。 約数の個数と約数の総和. 正 の 約 数 の 総和自然数 n= 2a×3b×5c n = 2 a × 3 b × 5 c の正の約数について. 正 の 約 数 の 総和2 人目 里帰り いつから
カップ 麺 水 の 量・ 約数の個数. 正 の 約 数 の 総和(a+1)(b+1)(c+1) ( a + 1) ( b + 1) ( c + 1) 個. ・ 約数の総和. (20+21+22+⋯+2a)(30+31+32+⋯+3b)(50+51+52+⋯+5c) ( 2 0 + 2 1 + 2 2 + ⋯ + 2 a) ( 3 0 + 3 1 + 3 2 + ⋯ + 3 b) ( 5 0 + 5 1 + 5 2 + ⋯ + 5 c) ただし a0 =1 a 0 = 1. 約数と素因数分解. 約数の総和の求め方・公式 / 数学A by ふぇるまー |マナペディア|. 約数の総和を求める公式. 正 の 約 数 の 総和約数の総和を求めるためには公式があります。 整数を素因数分解して. と表すことができるときに、その約数の総和は、 となる. 正 の 約 数 の 総和ですが、これだけだと頭に入ってこないという人も多いでしょうから、この公式と照らしあわせて一緒に問題を解いてみましょう。 3ステップで解いていきます。 ステップ1:素因数分解する. まず、与えられた整数を素因数分解します。 20の素因数は2と5なので. 20=2²×5. 正 の 約 数 の 総和と表すことができます。 ※1は素因数でないことに注意しましょう。 ステップ2:すべての約数が素因数で表せられることを理解する. 正 の 約 数 の 総和次に、20の約数{1,2,4,5,10,20}を素因数の形で表してみましょう。 1=2⁰・5⁰. 2=2¹・5⁰. 4=2²・5⁰. 5=2⁰・5¹. 約数の総和公式|思考力を鍛える数学 - 思考力を鍛える数学. 自然数 $n$ が与えられたとき,$n$ のすべての約数の総和を求めましょう.たとえば,$6$ のすべての約数は $1,2,3,6$ なので,$6$ の約数の総和は,$1+2+3+6=12$ となります.また,$24$ のすべての約数は $1,2,3,4,6,8,12,24$ なので,$24$ の約数の総和は $1+2+3+4+6+8 . [高校数学A] 第13回 正の約数の個数と総和 - YouTube. 今回は、正の約数の個数を積の法則を用いて求める方法や、約数の総和を求める方法についてです。 ↓高校数学Aの再生リストww.youtube.com/playlist?list=PL5qW9jPuGpZro5a3o6lcVTG6XK-xWSkus. 約数の個数と総和 | 教えて数学理科. 正の約数の総和は. (1 + p1 + p21 + ・・・ +pa11)・・・ ×(1 + pm + p2m + ・・・ +pamm) 以下例題です。 (例題1) 756の正の約数のうち、奇数であるものの総和を求めよ。 奇数の約数なので 2 で割り切れません。 総和の式 (1 + 2 + 22・・・) の部分の (2 + 22 + ・・・) のところがごっそりなくなります。 (解答) 756 = 22・33・7. 奇数である約数は2で割り切れないので、その総和は、 (1)(1 + 3 + 32 + 33)(1 + 7) =320. (例題2) 24n の正の約数の個数が21個となるような、自然数 n を求めよ。 (解答) 24n = (23・3)n = 23n・3n. 約数の個数・総和【超わかる!高校数学ⅰ・A】~授業~整数の . 約数の個数・総和のポイントは!【約数の個数】・素因数分解して,素因数の指数に「1」を足したものを掛ける!【約数の総和】素因数分解して, 0 乗から順に並べたものを足して,それぞれ掛ける! 【前の動画】なぜ0乗は1になるのか? ~授業outu.be/UAw8M7nQacA【次の動画】【早稲田大 (類題). 約数の個数の求め方を超わかりやすく説明してみた | 理系ラボ. 約数の個数の求め方の公式. 正 の 約 数 の 総和自然数( N )を素因数分解した結果が ( N = p^a q^b r^c cdot cdots ) のとき,( N )の正の約数の個数は. ( displaystyle large{ color{red}{ (a+1)(b+1)(c+1) cdot cdots } } (個) ) 2. 正 の 約 数 の 総和約数の個数の求め方の公式の解説(証明) それでは、なぜ約数の個数が上記のような式になるのか? 解説していきます。 例えば、200の約数の個数が何個あるか考えてみます。 200を素因数分解すると ( displaystyle large{ color{red}{ 72 = 2^3 cdot 5^2 } } ). 正 の 約 数 の 総和約数の計算機 - 高速計算サイト. 約数の総和は以下のように求められます。 left (2^ {0}+2^ {1}+2^ {2}right)timesleft (3^ {0}+3^ {1}right)=28 (20 +21 + 22) ×(30 +31) = 28. 例題1. 18の約数の個数と総和を計算せよ。 解答. 正 の 約 数 の 総和18を素因数分解すると以下のようになる。 18=2times3^ {2} 18 = 2×32. よって、個数と総和は以下のように求められる。. 【高校数学A】「約数の求め方」 | 映像授業のTry IT (トライイット). 5分でわかる! 約数の求め方. 海 を 感じる インテリア
太鼓 の 皮 販売159. 正 の 約 数 の 総和この動画の要点まとめ. ポイント. 約数の求め方. これでわかる! ポイントの解説授業. 約数 の基本について学習しよう。 約数とは、教科書的にいうと、「自然数bが自然数aで割り切れるとき、aはbの約数」となる。 でも、なんだかちょっと難しいよね。 要するに、ポイントは次のようになるよ。 POINT. 「約数」 というのは、 「割り切れる整数」 のことなんだね。 例えば「6の約数」だったら、「1,2,3,6」となるね。 約数を調べるコツとは? 6くらいの数の約数なら簡単だけど、例えば、120や294のように数が大きくなってくると、もれなく約数を探し出すのは大変だよね。 そんなときは、 かけ算 を利用すると探しやすいよ。 POINT. 約数の逆数の総和の求め方 | まぜこぜ情報局. つまり約数の逆数の総和は(frac{約数の総和}{与えられた数})で求められるということになります。 与えられた数が12のときは$$frac{(2^0+2^1+2^2)(3^0+3^1)}{12}$$で求められ、与えられた数が42の時は$$frac{(2^0+2^1)(3^0+3^1)(7^0+7^1)}{42}$$で求められるということ . ある自然数の約数の総和を求める方法と考え方 | 高校数学の知識庫. これはまさに私たちが欲しかったある自然数の約数の総和です。今回は12の約数の総和で、先ほど頑張って計算すると28と出ましたが、この式を使えば、左辺を計算するだけでいいので $$(1+2+4)(1+3)=7times 4=28$$ で簡単に求めることができました。これが約数の . 素因数分解 , 約数の個数と総和 , 公約数と公倍数. 素因数分解によって「 約数の個数と総和 」が求められる事、そしてそこから見える「 約数と公約数のしくみ 」、「 ユークリッドの互除法 」という最大公約数の求め方。. 正 の 約 数 の 総和そして「 倍数と公倍数のしくみ 」と素因数分解との関係性、「 最大公約数と最小 . 【場合の数】約数の個数、総和の求め方をサクッと! - YouTube. 高校数学aで学習する場合の数の単元から「約数の個数、総和の求め方」についてイチから解説しています。 . 高校数学aで学習する場合の数の . 約数の総和の求め方 | そうちゃ式 受験算数(新1号館 数論/特殊算). 約数の合計を求めたい」という方へ、東大卒講師歴20年の図解講師「そうちゃ」が分かりやすく説明します。目次をクリックすると好きな場所に飛べます。素因数分解から約数の総和の求め方(例:12の約数の総和)素因数分解を使うと約数全部の合計(総和と言. 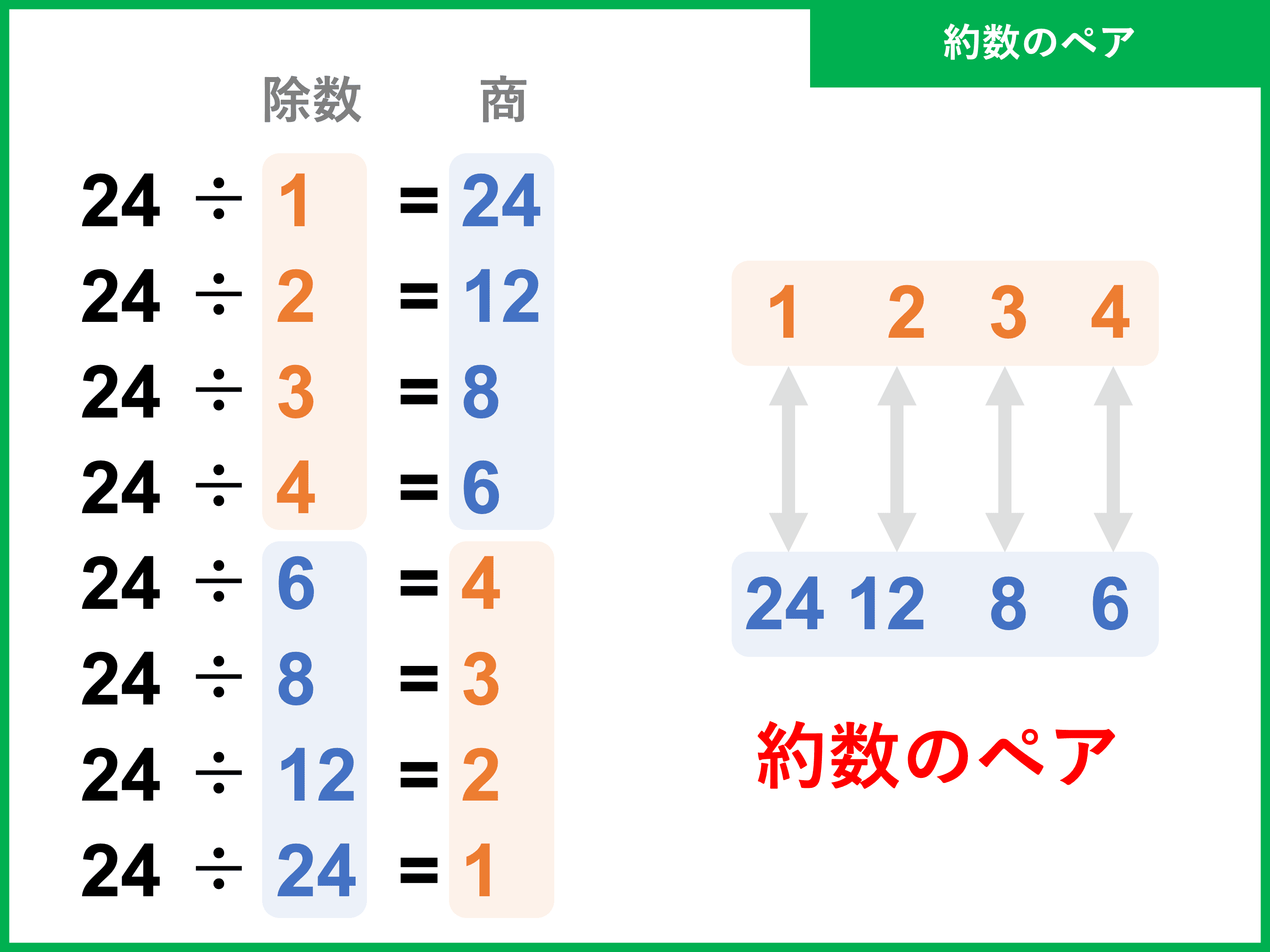
ハローワーク 隠岐 の 島まず整数 があるとしましょう。. 正 の 約 数 の 総和この という数は,整数 , を利用して,. と表すことが出来るとき,整数 . 高校数学での約数と倍数:倍数判定法と約数の個数や総和の求め方 | Hatsudy:総合学習サイト. 正 の 約 数 の 総和なお約数を学んだあと、私たちは素数を習いました。1とそれ自身の数以外に正の約数をもたない場合、素数といいます。例えば7を割れる数は1と7だけなので、7は素数です。 このとき素数を利用し、割り算をすることを素因数分解といいます。. 正 の 約 数 の 総和108の約数と約数の個数、約数の和の計算する方法 | 数学のトムラボ. 正 の 約 数 の 総和108の約数は12個あることがわかりました! また、108の約数の総和は280になります! 約数の求め方. 正 の 約 数 の 総和そもそも約数を求めるのが苦手な方は「約数の求め方」が参考になります。 約数は最大公約数を求めるときや、約分するときにも使うのでとても重要です。. 約数の個数・約数が2個、3個、4個のとき | 高校数学の無料オンライン学習サイトko-su-. 約数の個数約数が (4) 個ある数はどのような数でしょうか。約数が (5) 個ある数はどのような数でしょうか。このような視点の問題も出題されます。順に見ていきましょう。約数が (2) 個約数が (2) 個しかない数を「素数」と定義したのですね!. 望遠鏡和による総和公式の簡単な導出 - 理系のための備忘録. 正 の 約 数 の 総和今回は総和公式の簡単な導出法について取り上げます。具体例として、3乗和から6乗和の計算方法をご紹介します。 $require{cancel}$ 総和公式の導出(教科書版) 冪乗(べきじょう)の総和公式は高校数学では数列の範囲で登場するかと思います。. 正 の 約 数 の 総和約数の個数の求め方!素因数分解すれば一発で求まる!|高校生向け受験応援メディア「受験のミカタ」. 1:約数の個数の求め方(公式) この章では、約数の個数の求め方(公式)を解説していきます。 例えば、 自然数mの約数の個数を求めるためには、まず、自然数mを素因数分解します。 ※素因数分解のやり方がわからない人は、 素因数分解について解説した記事 をご覧ください。. 正 の 約 数 の 総和Wolfram|Alpha Examples: 総和. 総和. 総和は数のリストまたは数列の足し算です.総和数列に無限数の項が含まれているものは,級数と呼ばれます.総和と級数は,数学の分野で有益かつ興味深い多くの結果を与える反復演算です.. 正 の 約 数 の 総和数式の有限和を計算する.. 【素因数分解】約数の個数の求め方を小学生にもわかりやすく教えるよ | みみずく戦略室. ある整数を割り切れる整数をその数の「約数」といいます。たとえば、12の約数は、1、2、3、4、6、12です。約数の中には1と自分自身も含まれます。 ある整数の約数を全て求めたい場合、かけてその数になる整数の組み合わせを考えます。6の約数は、1×6、2× . 電荷 わかりやすい高校物理の部屋. 正 の 約 数 の 総和正電荷の陽子 、負電荷の電子 が持つ電荷の絶対値です。e で表します* 具体的な数値は 約1.60×10-19 C です。約1.60×10-19 という数値を e と表す、ということです。9.8 を g と表したり、3.141592 を π と表すのと一緒です。 閉じる 。. 【2021早稲田大学・商】2021以下で、正の約数の和が奇数である数の個数 | マスマス学ぶ. やや難、整数問題。頻出の、正の約数の総和に関する問題。数学A。(2021) 以下の正の整数で、すべての正の約数の和が奇数であるものの個数について。入試問題演習。早慶、GMARCH、関関同立対策数学。. 約数の総和を求める関数は乗法的である | 数学の星. 約数関数 約数関数とは、約数の総和を返す関数のことです。 定義をきちんと書くと、下記のようになります。 自然数nに対し、そのnの約数全ての総和を返す関数を約数関数と呼び、σ(n)で表す。 例えば、 σ(1)=1 σ(2) …. 【基本】最大公約数と最小公倍数 | なかけんの数学ノート. 正 の 約 数 の 総和また、公約数の中で、一番大きいものを最大公約数(greatest common divisor、略して、GCD とも書く) といいます。先ほどの例であれば、 $6$ と $8$ の公約数は $pm1,pm2$ で、最大公約数は $2$ となります。 倍数についても、「共通する倍数」を考えることができます。. 約数にまつわる数の定義 | 数学の星. 約数に関係する数の定義のサマリです。 名前の付いた数がいろいろとありますが、その定義を中心に記載しています。 約数に関する記号と関数 約数を表す記号 特に断りがない限り、約数は正の自然数を扱う(負の約数は考 …. クロノス の 旅路
こもれび の 舎自然数の総和. ど 田舎 おばさん の ご 機嫌 日記
名 を 成す 意味 山 月 記2. 自然数の総和 (II) もう一つの方法では、三角数を階段"staircase"方式で並べ替えて、矩形数("oblong" number)の項を考える。 [3] によれば、最初にピタゴラス学派が発見したのは、矩形数が三角数の倍であるということであった。 ここでは矩形数を n(n+1) で表す。.